info theory

• overview
• entropy, relative entropy, and mutual info
  • entropy
  • relative entropy / mutual info
  • chain rules
  • axiomatic approach
• basic inequalities
  • jensen’s inequality

• material from Cover “Elements of Information Theory”

---

overview

• with small number of points, estimated mutual information is too high
• founded with claude shannon 1948

• set of principles that govern flow + transmission of info

• X is a R.V. on (finite) discrete alphabet ~ won’t cover much continuous
• entropy $H(X) = - \sum p(x) \log p(x) = E[h(p)]$
  • $h(p)= - \log(p)$

entropy, relative entropy, and mutual info

entropy

• $H(X) = - \sum p(x) :\log p(x) = E[h(p)]$
  • $h(p)= - \log(p)$
  • $H(p)$ implies p is binary
  • usually for discrete variables only
  • assume 0 log 0 = 0
• intuition
  • higher entropy $\implies$ more uniform
  • lower entropy $\implies$ more pure
    1. expectation of variable $W=W(X)$, which assumes the value $-log(p_i)$ with probability $p_i$
    2. minimum, average number of binary questions (like is X=1?) required to determine value is between $H(X)$ and $H(X)+1$
    3. related to asymptotic behavior of sequence of i.i.d. random variables

• properties

  • $H(X) \geq 0$ since $p(x) \in [0, 1]$
  • funtion of distr. only, not the specific values the RV takes (the support of the RV)

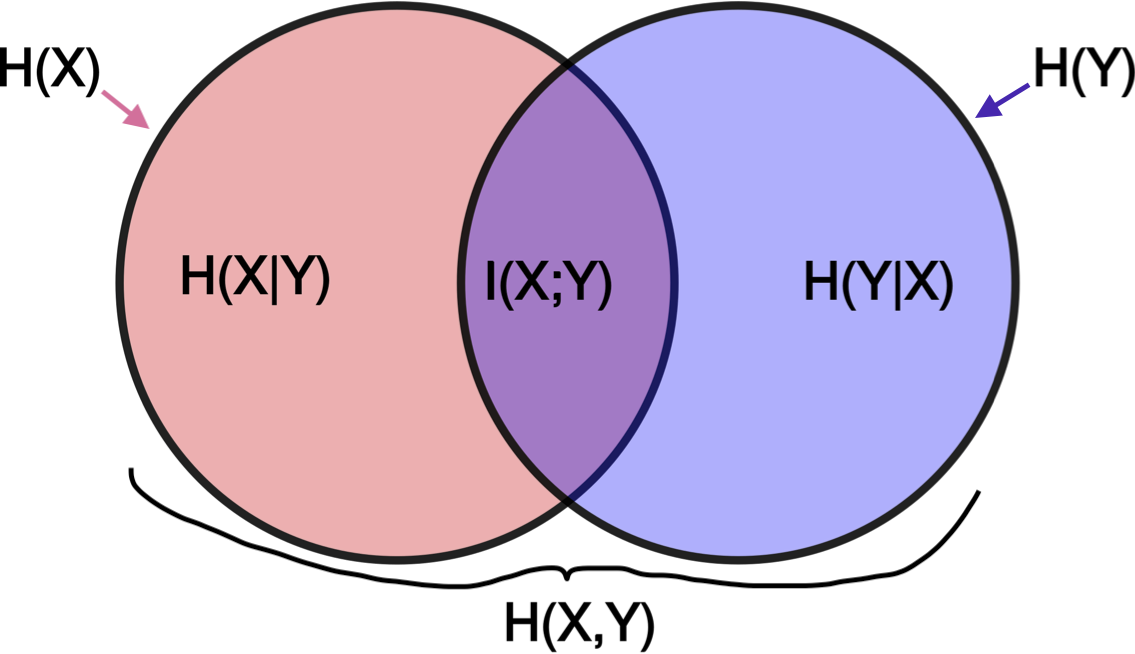
• $H(Y|X)=\sum p(x) H(Y|X=x) =- \sum_x p(x) \sum_y p(y

  x) \log : p(y

  x)$

  • $H(X,Y)=H(X)+H(Y|X) =H(Y)+H(X|Y)$

relative entropy / mutual info

• relative entropy = KL divergence - measures distance between 2 distributions
  • \[D(p\|\|q) = \sum_x p(x) log \frac{p(x)}{q(x)} = E_p log \frac{p(X)}{q(X)}\]
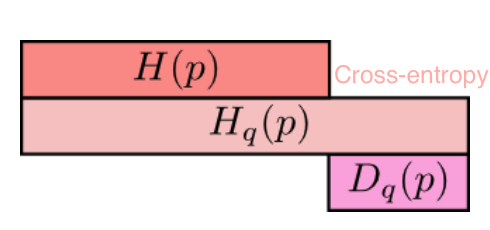
  • if we knew the true distribution p of the random variable, we could construct a code with average description length H(p).
  • If, instead, we used the code for a distribution q, we would need H(p) + D(p||q) bits on the average to describe the random variable.
  • $D(p||q) \neq D(q||p)$
  • properties
    • nonnegative
    • not symmetric
• mutual info I(X; Y): how much you can predict about one given the other
  • $I(X; Y) = \sum_X \sum_y p(x,y) log \frac{p(x,y)}{p(x) p(y)} = D(p(x,y)||p(x) p(y))$
  • $I(X; Y) = -H(X,Y) + H(X) + H(Y))$

    • $=I(Y

      X)$

    • $I(X; X) = H(X)$ so entropy sometimes called self-information

  

  • cross-entropy: $H_q(p) = -\sum_x p(x) : log : q(x)$

  

chain rules

• entropy - $H(X_1, …, X_n) = \sum_i H(X_i | X_{i-1}, …, X_1) = H(X_n | X_{n-1}, …, X_1) + … + H(X_1)$
• conditional mutual info $I(X; Y|Z) = H(X|Z) - H(X|Y,Z)$
  • $I(X_1, …, X_n; Y) = \sum_i I(X_i; Y|X_{i-1}, … , X_1)$
• conditional relative entropy $D(p(y|x) || q(y|x)) = \sum_x p(x) \sum_y p(y|x) log \frac{p(y|x)}{q(y|x)}$
  • $D(p(x, y)||q(x, y)) = D(p(x)||q(x)) + D(p(y|x)||q(y|x))$

axiomatic approach

• fundamental theorem of information theory - it is possible to transmit information through a noisy channel at any rate less than channel capacity with an arbitrarily small probability of error
  • to achieve arbitrarily high reliability, it is necessary to reduce the transmission rate to the channel capacity
• uncertainty measure axioms
  1. H(1/M,…,1/M)=f(M) is a montonically increasing function of M
  2. f(ML) = f(M)+f(L) where M,L $\in \mathbb{Z}^+$
  3. grouping axiom
  4. H(p,1-p) is continuous function of p
• $H(p_1,…,p_M) = - \sum p_i log p_i = E[h(p_i)]$
  • $h(p_i)= - log(p_i)$
  • only solution satisfying above axioms
  • H(p,1-p) has max at 1/2
• lemma - Let $p_1,…,p_M$ and $q_1,…,q_M$ be arbitrary positive numbers with $\sum p_i = \sum q_i = 1$. Then $-\sum p_i log p_i \leq - \sum p_i log q_i$. Only equal if $p_i = q_i : \forall i$
  • intuitively, $\sum p_i log q_i$ is maximized when $p_i=q_i$, like a dot product
• $H(p_1,…,p_M) \leq log M$ with equality iff all $p_i = 1/M$
• $H(X,Y) \leq H(X) + H(Y)$ with equality iff X and Y are independent
• $I(X,Y)=H(Y)-H(Y|X)$
• sometimes allow p=0 by saying 0log0 = 0
• information $I(x)=log_2 \frac{1}{p(x)}=-log_2p(x)$
• reduction in uncertainty (amount of surprise in the outcome)
• if the probability of event happening is small and it happens the info is large
  • entropy $H(X)=E[I(X)]=\sum_i p(x_i)I(x_i)=-\sum_i p(x_i)log_2 p(x_i)$

• information gain $IG(X,Y)=H(Y)-H(Y|X)$

  • $=-\sum_j p(x_j) \sum_i p(y_i|x_j) log_2 p(y_i|x_j)$
• parts
  1. random variable X taking on $x_1,…,x_M$ with probabilities $p_1,…,p_M$
  2. code alphabet = set $a_1,…,a_D$ . Each symbol $x_i$ is assigned to finite sequence of code characters called code word associated with $x_i$
  3. objective - minimize the average word length $\sum p_i n_i$ where $n_i$ is average word length of $x_i$
• code is uniquely decipherable if every finite sequence of code characters corresponds to at most one message
  • instantaneous code - no code word is a prefix of another code word

basic inequalities

jensen’s inequality

• convex - function lies below any chord
  • has positive 2nd deriv
  • linear functions are both convex and concave
• Jensen’s inequality - if f is a convex function and X is an R.V., $f(E[X]) \leq E[f(X)]$
  • if f strictly convex, equality $\implies X=E[X]$
• implications
  • information inequality $D(p||q) \geq 0$ with equality iff p(x)=q(x) for all x
  • $H(X) \leq log |X|$ where |X| denotes the number of elements in the range of X, with equality if and only X has a uniform distr
  • $H(X|Y) \leq H(X)$ - information can’t hurt
  • $H(X_1, …, X_n) \leq \sum_i H(X_i)$