causal inference

• causality (freedman ch 1)
• basic causal inference
• causal inference papers
• causality ovw

---

causality (freedman ch 1)

• When using observational (non-experimental) data to make causal inferences, the key problem is confounding
  • stratification = cross-tabulation - only look at when confounding variables have same value
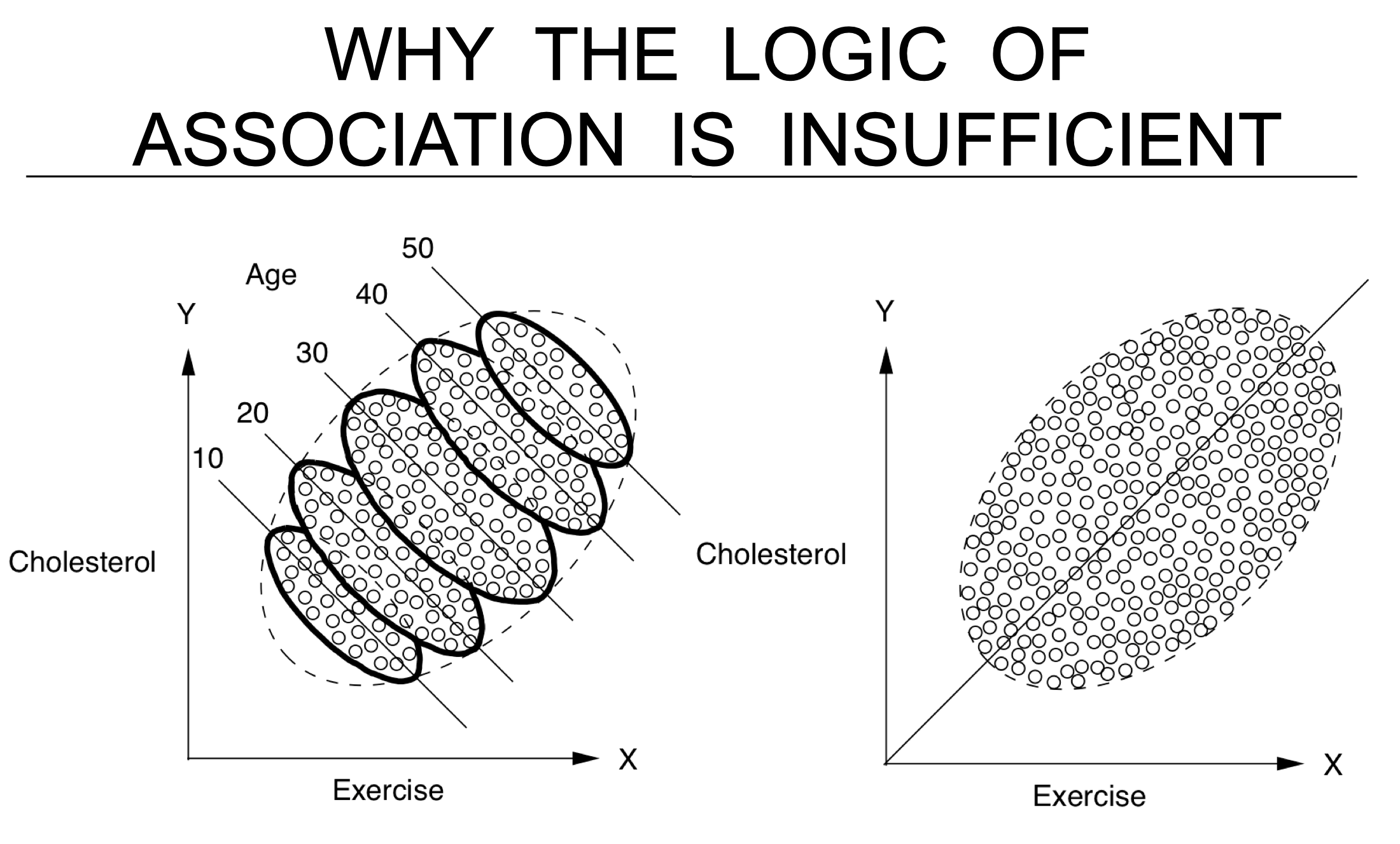
• association is circumstantial evidence for causation
• examples
  • HIP trial of mammography - want to do whole treatment group v. whole control group
  • Snow on cholera - water
  • causes of poverty - Yul’s model, changes with lots of things
• problem: never get to see gt

basic causal inference

• confounding - difference between groups other than the treatment which affects the response
• 3 frameworks
  1. neyman-rubin model: $Y_i = T_i a_i + (1-T_i) b_i$
     • $\hat{ate} = \hat{a}_A - \hat{b}_B$
     • $\hat{ate}_{adj} = [\bar{a}_A - (\bar{x}_A - \bar{x})^T \hat{\theta}_A] - [\bar{b}_B - (\bar{x}_B - \bar{x})^T \hat{\theta}_B]$
     • $\hat{\theta}A = argmin \sum{i \in A} (a_i - \bar{a}_A - (x_i - \bar{x}_A)^T \theta)^2$
  2. neyman-pearson
     • null + alternative hypothesis
     • null is favored unless there is strong evidence to refute it
  3. fisherian testing framework
     • small p-values evidence against null hypothesis
     • null hypothesis
• errors
  • type I err: FP - reject when false
  • type II err: FN
  • power: TP = sensitivity
  • TN
  • newer
    • sensitivity = power
    • recall = sensitivity - true positive rate = TP / P
    • precision = TP / (TP + FP)
    • specificity = true neg rate = TN / N
• natural experiments
  • ex. john snow
• propensity score - probability that a subject recieving a treatment is valid after conditioning on appropriate covariates
• 3 principles of experimental design
  1. replication
  2. randomization
  3. conditioning

causal inference papers

• 2 general approaches
  1. matching - find patients that are similar and differ only in the treatment
     1. only variables you don’t match on could be considered causal
  2. regression
     • requires unconfoundedness = omitted variable bias
     • if there are no confounders, correlation is causation
• Hainmueller & Hangartner (2013) - Swiss passport
  • naturalization decisions vary with immigrants’ attributes
  • is there immigration against immigrants based on country of origin?
  • citizenship requires voting by municipality
• Sekhon et al. - when natural experiments are neither natural nor experiments
  • even when natural interventions are randomly as- signed, some of the treatment–control comparisons made available by natural experiments may not be valid
• Grossman et al. - “Descriptive Representation and Judicial Outcomes in Multiethnic Societies”
  • judicial outcomes of arabs depended on whether there was an Arab judge on the panel
• liver transplant
  • maximize benefit (life with - life without)
  • currently just goes to person who would die quickest without
  • Y = T Y(1) + (1-T) Y(0)
    • Y(1) = survival with transplant
    • Y(0) = survival w/out transplant
      • fundamental problem of causal inference - can’t observe Y(1) and Y(0)
    • T = 1 if receive transplant else 0
  • goal: estimate $\tau = Y(1) - Y(0)$ for each person

causality ovw