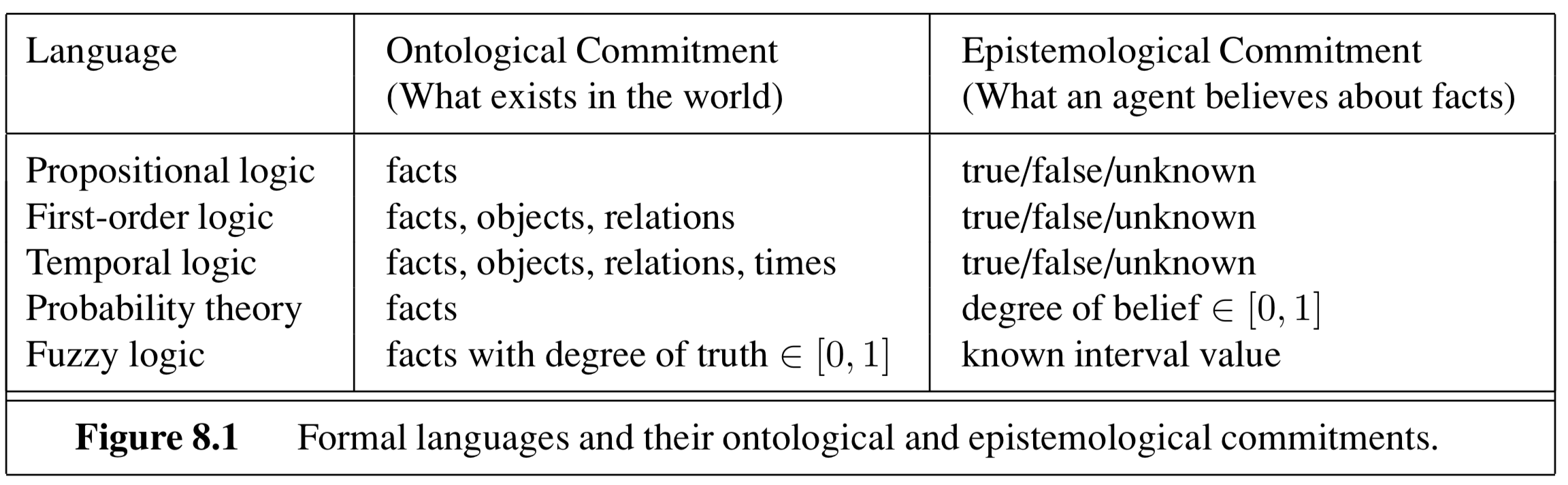
logical agents - 7.1-7.7 (omitting 7.5.2)

knowledge-based agents - intelligence is based on reasoning that operates on internal representations of knowledge
3 steps: given a percept, the agent
1. adds the percept to its knowledge base (KB)
2. asks the knowledge base for the best action
3. tells the knowledge base that it has taken that action
2 approaches
- declarative approach - tell sentences until agent knows how to operate
  - know something, can verbalize it
- procedural approach - encodes desired behaviors as program code
  - intuitively know how to do it (ex. riding a bike)
ex. Wumpus World
logical entailment between sentences
- $A \vDash B$ means B follows logically from A (A implies B)
- logical inference - showing entailment
model checking - try everything to see if A $\implies$ B
- this is sound = truth-preserving
- complete - can derive any sentence that is entailed
- TT-ENTAILS
  - recursively enumerate all sentences by assigning true, false to each variable
  - check if these are valid within the KB
    - if they are, they must also match the query (otherwise return false)
grounding - connection between logic and real environment (usually sensors)
theorem properties
- validity - tautalogy - true under all models
- satisfiable - true under some model
  - ex. boolean-SAT
- monotonicity - set of implications can only increase as info is added to the knowledge base
  - if $KB \implies A$ then $KB \land B \implies A$

theorem proving

resolution rule - resolves different rules with each other - leads to complete inference procedure
CNF - conjunctive normal form - conjunction (and) of clauses (with ors)
- ex: $ ( \neg A \lor B) \land \neg C \land (D \lor E)$
- anything can be expressed as this
horn clause - at most one positive
- definite clause - disjunction of literals with exactly one positive: ex. ($A \lor \neg B \lor \neg C$)
- goal clause - no positive: ex. ($\neg A \lor \neg B \lor \neg C$)
- benefits
  - easy to understand
  - forward-chaining / backward-chaining are applicable
  - deciding entailment is linear in size (KB)
- forward/backward chaining: checks if q is entailed by KB of definite clauses
  - data-driven
  - keep adding until query is added or nothing else can be added
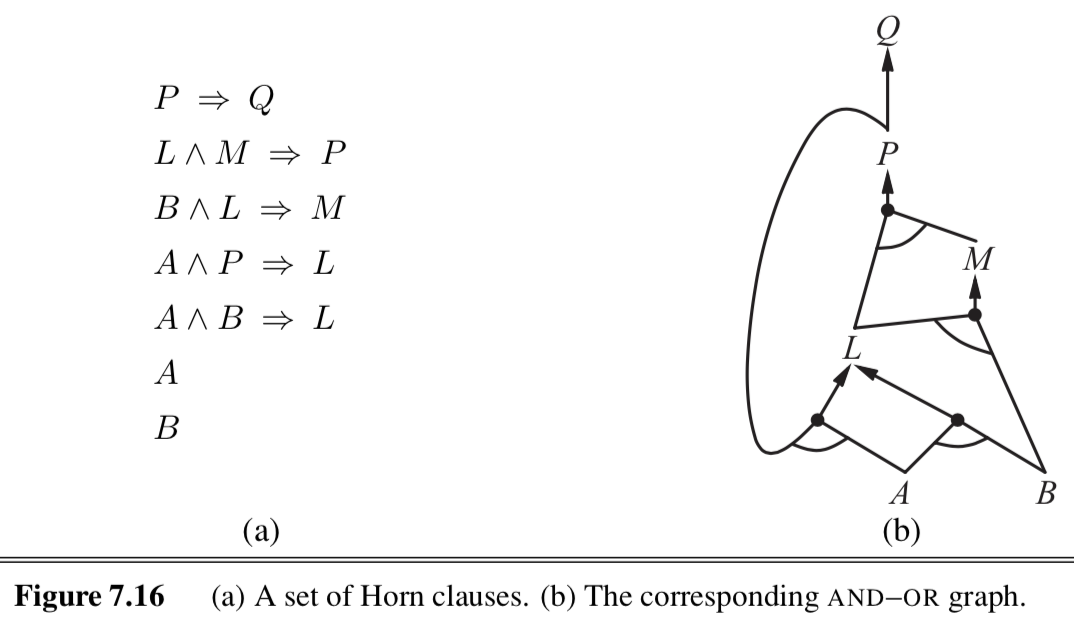
  - backward chaining works backwards from the query
    - goal-driven
    - keep going until get back to known facts
checking satisfiability
- complete backtracking
  - davis-putnam algorithm = DPLL - like TT-entails with 3 improvements
    1. early termination
    2. pure symbol heuristic - pure symbol appears with same sign in all clauses, can just set it to the proper value
    3. unit clause heuristic - clause with just one literal or one literal not already assigned false
  - other improvements (similar to search)
    1. component analysis
    2. variable and value ordering
    3. intelligent backtracking
    4. random restarts
    5. clever indexing
- local search
  - evaluation function can just count number of unsatisfied clauses (MIN-CONFLICTS algorithm for CSPs)
  - WALKSAT - randomly chooses between flipping based on MIN-CONFLICTS and randomly
    - runs forever if no soln
- underconstrained problems are easy to find solns
- satisfiability threshold conjecture - for random clauses, probability of satisfiability goes to 0 or 1 based on ratio of clauses to symbols
  - hardest problems are at the threshold

agents based on propositional logic

fluents = state variables that change over time
can index these by time
effect axioms - specify the effect of an action at the next time step
frame axioms - assert that all propositions remain the same under actions
succesor-state axiom: $F^{t+1} \iff ActionCausesF^t \lor (F^t \land -ActionCausesNotF^t )$
- ex. $HaveArrow^{t+1} \iff (HaveArrow^t \land \neg Shoot^t)$
- makes things stay the same unles something changes
state-estimation: keep track of belief state
can just use 1-CNF (conjunctions of literals: ex. $WumpusAlive \land L_2 \and B$)
- 1-CNF includes all states that are in fact possible given the full percept history
- conservative approximation - contains belief state, but also extraneous stuff
planning
- could use $A^*$ with entailment
- otherwise, could use SATPLAN
SATPLAN - how to make plans for future actions that solve the goal by propositional inference
basic idea
- make assertions
- transitions up to some max time $t_{final}$
- assert that goal is achieved at time $t_{final}$ (ex. havegold)
present this to a SAT solver
- must add precondition axioms - states that action occurrence requires preconditions to be satisfied
  - ex. can’t shoow without arrow
- must add action exclusion axioms - one action at a time
  - ex. can’t shoot and move at once

first-order logic - 8.1-8.3.3

basically added objects, relations, quantifiers ($\exists, \forall$)
declarative language - semantics based on a truth relation between sentences and possible worlds
- has compositionality - meaning decomposes
- sapir-whorf hypothesis - understanding of the world is influenced by the language we speak
3 elements
1. objects - john (cannot appear by itself, need boolean value)
2. relations - set of tuples (ex. brother(richard, john))
3. functions - only one value for given input (ex. leftLeg(john))
sentences return true or false
- combine these things
first-order logic assumes more about the world than propositional logic
- epistemological commitments - the possible states of knowledge that a logic allows with respect to each fact
- higher-order logic - views relations and functions as objects in themselves
first-order consists of symbols
1. constant symbols - stand for objects
2. predicate symbols - stand for relations
3. function symbols - stand for functions
  - arity - fixes number of args
  - term - logical expresision tha refers to an object
  - atomic sentence - formed from a predicate symbol optionally followed by a parenthesized list of terms
    - true if relation holds among objects referred to by the args
    - ex. Brother(Richard, John)
  - interpretation - specifies exactly which objects, relations and functions are referred to by the symbols

inference in first-order logic - 9.1-9.4

propositionalization - can convert first-order logic to propositional logic and do propositional inference
- universal instantiation - we can infer any sentence obtained by substituting a ground term for the variable
  - replace “forall x” with a specific x
- existential instantiation - variable is replaced by a new constant symbol
  - replace “there exists x” with a specific x that give a name (called the Skolem constant)
- only need finite subset of propositionalized KB - can stop nested functions at some depth
  - semidecidable - algorithms exist that say yes to every entailed sentence, but no algorithm exists that also says no to every nonentailed sentence
generalized modus ponens
unification - finding substitutions that make different logical expressions look identical
- UNIFY(Knows(John,x), Knows(x,Elizabeth)) = fail .
  - use different x’s - standardizing apart
  - want most general unifier
- need occur check - S(x) can’t unify with S(S(x))
storage and retrieval
- STORE(s) - stores a sentence s into the KB
- FETCH(q) - returns all unifiers such that the query q unifies with some sentence in the KB
  - only try to unify reasonable facts using indexing
  - query such as Employs(IBM, Richard)
  - all possible unifying queries form subsumption lattice
forward chaining: start w/ atomic sentences + apply modus ponens until no new inferences can be made
- first-order definite clauses - (remember this is a type of Horn clause)
- Datalog - language restricted to first-order definite clauses with no function symbols
- simple forward-chaining: FOL-FC-ASK - may not terminate if not entailed
  1. pattern matching is expensive
  2. rechecks every rule
  3. generates irrelevant facts
- efficient forward chaining (solns to above problems)
  1. conjuct odering problem - find an ordering to solve the conjuncts of the rule premise so the total cost is minimized
    - requires heuristics (ex. minimum-remaining-values)
  2. incremental forward chaining - ignore redundant rules
    - every new fact inferred on iteration t must be derived from at least one new fact inferred on iteration t-1
    - rete algorithm was first to do this
  3. irrelevant facts can be ignored by backward chaining
    - could also use deductive database to keep track of relevant variables
backward-chaining
- simple backward-chaining: FOL-BC-ASK
  - is a generator - returns multiple times, each giving one possible result
- like DFS - might go forever
- logic programming: algorithm = logic + control
  - ex. prolog
  - a lot more here
  - can have parallelism
  - redudant inference / infinite loops because of repeated states and infinite paths
  - can use memoization (similar to the dynamic programming that forward-chaining does)
  - generally easier than converting it into FOLD
- constraint logic programming - allows variables to be constrained rather than bound
  - allows for things with infinite solns
  - can use metarules to determine which conjuncts are tried first

classical planning 10.1-10.2

planning - devising a plan of action to achieve one’s goals
Planning Domain Definition Language (PDDL) - uses factored representation of world
- closed-world assumption - fluents that aren’t present are false
- solving the frame problem: only specify result of action in terms of what changes
- requires 4 things (like search w/out path cost function)
  - initial state
  - actions
  - transitions
  - goals
- no quantifiers
set of ground (variable-free) actions can be represented by a single action schema
- like a method with precond and effect
- $Action(Fly(p, from, to))$:
  - PRECOND: $At(p, from) \land Plane(p) \land Airport(from) \land Airport(to)$
  - EFFECT: $\neg At(p, from) \land At(p, to)$
    - can only use variables in the precondition
problems
- PlanSAT - try to find plan that solves a planning problem
- Bounded PlanSAT - ask whether there is a soln of length k or less

algorithms for planning as state-space search

forward (progression) state-space search
- very inefficient
- generally forward search is preferred because it’s easier to come up with good heuristics
backward (regression) relevant-states search
- PDLL makes it easy to regress from a state description to the predecessor state description
- start with a set of things in the goal (and any other fluent can hae any value)
  - keep track of a set at all points
- in going backward, the effects that were added need not have been true before, but preconditions must have held before
heuristics
- ex. ignore preconditions
- ex. ignore delete lists - remove all negative literals
- ex. state abstractions - many-to-one mapping from states $\to$ abstract states
  - ex. ignore some fluents
decomposition
- requires subgoal independence